
|
Автор |
Тема: Задачки, разминаемся. (Прочитано 401290 раз)
|
| 0 Пользователей и 1 Гость смотрят эту тему.
|
kondr
Активный участник
 
Карма: +0/-0
 Offline Offline
Сообщений: 199
|
Вспомнилась задача со школьных времён... Оказание первой помощи при артериальном кровотечении... Наложить жгут... Помним, конечно. Задача: артериальное кровотечение, - височное ранение. Как будем накладывать?  Предплече, противоположное разбитому виску, кладется на макушку, плечо принимает вертикальное положение, жгут зажимает артерию со стороны виска.
|
|
|
|
|
 Записан
Записан
|
|
|
|
kondr
Активный участник
 
Карма: +0/-0
 Offline Offline
Сообщений: 199
|
И ещё нашла задачку: Давным-давно жил-был старик, который, умирая, оставил своим трем сыновьям 19 верблюдов. Он завещал старшему сыну половину, среднему - четвертую часть, а младшему - пятую. Не сумев найти решения самостоятельно, братья обратились к мудрецу.
- О, мудрец! - сказал старший брат. - Отец оставил нам 19 верблюдов и велел разделить между собой: старшему половину, среднему -четверть, младшему - пятую часть. Но 19 не делиться ни на 2, ни на 4, ни на 5. Можешь ли ты, о достопочтенный, помочь нашему горю, ибо мы хотим выполнить волю отца?
- Нет ничего проще, - ответил им мудрец...........я даю вам одного верблюда, т.о. старший получит 10 верблюдов, средний 5, младший 4. Остается один верблюд и я забираю его себе 
|
|
|
|
|
 Записан
Записан
|
|
|
|
kondr
Активный участник
 
Карма: +0/-0
 Offline Offline
Сообщений: 199
|
Зверь бежит-шкура лежит
Электрический ток?
|
|
|
|
|
 Записан
Записан
|
|
|
|
Steel
Профи
Старожил
    
Карма: +17/-3
 Offline Offline
Сообщений: 3560
|
Зверь бежит-шкура лежит
Электрический ток?
А может струя воды из шланга... (дети про ток откуда знают?)
|
|
|
|
|
 Записан
Записан
|
|
|
|
Aleks
Профи
Старожил
    
Карма: +604/-39
 Offline Offline
Сообщений: 8110
|
Зверь бежит-шкура лежит
Электрический ток?
Сам зверь бежит, а шкура на нём лежит))
|
|
|
|
|
 Записан
Записан
|
|
|
|
Aleks
Профи
Старожил
    
Карма: +604/-39
 Offline Offline
Сообщений: 8110
|
Насчёт птички, вес не меняется.
з.ы. Авиационное Техническое Училище Гражданской Авиации заканчивал, аэродинамику помню, немного)))
|
|
|
|
|
 Записан
Записан
|
|
|
|
Гoсть
Гость

|
KM, спасибо за разъяснения. Теперь я полностью понял Вашу точку зрения и постараюсь объяснить где я вижу в ней ошибку. Могу, если есть желание, также разложить по пунктам своё видение процессов, чтобы вы указали мою ошибку.
1. Давайте сразу условимся, что не будем рассматривать неуравновешенную систему, где вносятся какие-либо предметы извне или где что-то движется с ускорением.
Я согласен с тем, что мы не будем рассматривать систему в момент начала или окончания каких-то движений. Момент взлета или приземления не рассматриваем. Но по поводу ускорения ситуация иная. Вы сами пишете чуть ниже про ракету: " берем случай, когда ракета уже находится в полете (висит на определенном расстоянии, не опускаясь и не поднимаясь - т.е. без ускорения, т.к. только в этом случае вес равен произведению массы на g).
Совершенно очевидно, что для выполнения этого условия ракета должна иметь собственное ускорение a, равное g (противоположное по направлению, но рассматривать будем модули для простоты)." Вы не находите противоречия в своей фразе? В первой части ракета висит без ускорения, а во второй для этого условия нужно ускорение? Именно отсюда и возникает ошибка. Чтобы висеть в воздухе требуется ускорение направленное противоположно g. Или другими словами, пока в системе что-то летает, ускорение есть по определению. Мы можем не рассматривать момент взлета и посадки, но в момент полета ускорение будет. Именно из-за этого ускорения, которое компенсирует (в той или иной степени) g и исчезает реакция на опору, то есть внешний вес. Пример неуравновешенной системы из нашей задачи: птицы сидят на дне. Затем взлетают (отталкиваются от дна). В этот момент давление на дно лапами и воздухом крыльев будет высоким, и вес системы увеличится (весы это зафиксируют). Затем птицы взмывают в высоту, и создаваемое ими давление на воздух еще не дошло до дна (потому что воздух упругий). Вес системы уменьшится. Это тоже неуравновешенная система.
Отмечу, что формально, описываемая ситуация уже подходит под условия задачи. Внешний вес системы изменится когда птицы взлетели, что собственно и спрашивалось. Но я не буду придираться, а доведу дело до условно стабильной ситуации, когда птица продолжительное время висит в воздухе работая крыльями. Промежутки времени, когда система не уравновешена, мы рассматривать не будем, т.к. это не соответствует условию задачи. Если говорить в общем смысле и рассматривать систему на протяжении всего времени, то да, найдутся интервалы времени, в течение которых вес системы будет колебаться вверх/вниз по причине ее неуравновешенности (из-за движения с ускорением). С этим я не спорю!
Формально, повторюсь, условию задачи это соответствует. Но пойдем дальше. Очень приятно осознавать, что вы не спорите с тем, что в момент, когда на тело внутри системы действует ускорение вес может меняться. Мне осталось только объяснить, что полет и есть движение с ускорением. Весьма непродолжительный если действует g (падение после взлета) или затянутый, когда тело себя в воздухе поддерживает. 2. Объясняю, в чем неверное понимания закона Паскаля Александром и Гостем (в особенности  ). "Локальных зон" в нашей системе не существует, т.к. мы договорились не рассматривать неуравновешенную систему. Теперь смотрите на картинку. Вы пытаетесь применить закон Паскаля ко всему цилиндру, но это неверно! Цилиндр разделен птицей на две части. Вот тут стоп. Почему это разделен? В задаче есть контейнер (априори нечто достачно большое по объему) и канарейки (априори мелкое). Второй пример с колибри и колпаком тоже показывает разницу в размерах на порядки. На приведенных вами картинках - птица по сути является поршнем, а в реальности ситуация прямо противоположная. Зоны избыточного и низкого давления как раз и будут локальными, поскольку растояние от птицы до стен на порядки больше её размеров и размеров создаваемой зоны высокого/низкого давления. Может быть наше взаимное непонимание именно тут? Вы рассматривали птицу как поршень, а я как практически материальную точку? Если да, то следует выяснить, какая из трактовок ближе к условиям задачи. Согласны? --- Далее я сразу перескочу к ракете, а потом вернусь к птице. Ошибку с ускорением я уже указал. Выводы о поведении ракеты я опускаю, там спорить особо не с чем. Отмечу только вот эти ваши фразы: Таким образом, еще раз подтверждена формула: в уравновешенной системе P=m*g. Всегда.
Вот! Для Вас, уравновешенная система это когда ничего не движется. Когда всё уже жестко взаимодействует. Когда у всего есть реакция опоры и нет ускорения. Но полет-то, как вы сами сказали, требует ускорения. В условиях задачи оговаривается момент измерения "когда взлетели". Заметьте! Не когда толкнулись, не когда сели обратно, легли и заснули, а когда взлетели (и, предположительно, когда еще летят). А в этот момент система не может быть уравновешена по определению. Вместо шариков могут быть молекулы газа, это не играет никакой роли, т.к. на молекулы точно так же воздействует сила тяжести и они полетят вниз в вакууме по той же формуле.
В вакууме может быть. Но в газовой среде всё совсем по другому. В неком приближении (газовая динамика это статистическая механика массы крайне маленьких шариков-молекул), птица берет "шарики" (молекулы) из окружающей среды и кидает их вниз. Тем самым отталкивается. Но только шарики в среде не падают вниз, а перетекают (привет Паскаль!) обратно в ту область откуда их взяли. Единственное, что я могу признать в "реальной модели" - это то, что система будет чуть легче за счет того, что шарики не мгновенно упадут на дно, а будут находиться в полете. Но это скомпенсируется в тот момент, когда все шарики будут на дне, а ракета будет падать.
Вот тут мы и приходим к взаимопониманию. Если птица не является поршнем (надеюсь, что я это объяснил исходя из условий задачи), то заменив шарики на молекулы воздуха и поняв, что они не будут падать как дробинки, а начнут поступать в зону разрежения (то есть образуется локальный круговорот отбрасываемой массы), мы придем к тому, что полет будет длиться до тех пор, пока у птицы есть кинетическая энергия, которую она расходует на создание ускорения против g. И ни на что она при этом не опирается (опора возможна только на несжимаемое тело). Я споры не прекращаю, пока. Уважаемые оппоненты, пожалуйста, не давайте "голых" объяснений, а укажите на ошибку в моих рассуждениях, как я указал на ошибки в объяснениях КМ. Взаимные (возможно, что и взаимноошибочные) объяснения - путь в тупик. Спасибо за внимание
|
|
|
|
|
 Записан
Записан
|
|
|
|
KM
Профи
Старожил
    
Карма: +604/-10
 Offline Offline
Сообщений: 2654
|
Да, в фразе "Берем случай, когда ракета уже находится в полете (висит на определенном расстоянии, не опускаясь и не поднимаясь - т.е. без ускорения, т.к. только в этом случае вес равен произведению массы на g)" я действительно допустил опечатку, имелось в виду "без движения". Всё остальное верно.
|
|
|
|
|
 Записан
Записан
|
|
|
|
Гoсть
Гость

|
Да, в фразе "Берем случай, когда ракета уже находится в полете (висит на определенном расстоянии, не опускаясь и не поднимаясь - т.е. без ускорения, т.к. только в этом случае вес равен произведению массы на g)" я действительно допустил опечатку, имелось в виду "без движения". Всё остальное верно.
Мы скоро договоримся!  Без движения (в системе отсчета относительно пола контейнера, я правильно понял?) можно находиться в двух случаях. Или опираясь на не сжимаемое тело, или двигаясь с ускорением равным g и направленным противоположно. Согласны? И что скажете по поводу размеров птицы и контейнера?
|
|
|
|
|
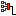 Записан
Записан
|
|
|
|
Гoсть
Гость

|
Насчёт птички, вес не меняется.
з.ы. Авиационное Техническое Училище Гражданской Авиации заканчивал, аэродинамику помню, немного)))
Уважаемый, может быть вы сможете указать ошибку в моих построениях?
|
|
|
|
|
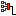 Записан
Записан
|
|
|
|
Steel
Профи
Старожил
    
Карма: +17/-3
 Offline Offline
Сообщений: 3560
|
хм.. я озадачен. Честно.
Если прав КМ, это значит, что птица полностью опирается на дно вагона. А я вот думаю, что даже если давление внизу вагона и выше, чем наверху (хоть на чуточку), то это не значит что воздух давит только на пол вагона. Он по идее должен также давить сильнее и на стенки вагона, в участках ниже от птицы. Т.е. опорой птицы может являться упругое сопротивление стенок вагона, которое никак не отражается на показаниях весов... А площадь стен больше чем дно вагона. потому вес должен существенно снизится...
если бы две противоположных стенки вагона были из тонкой резины а вместо канарейки был бы вертолетик тяжелый, но небольших размеров, то как мне кажется, из-за сильного давления снизу стенки вагона раздвинулись бы. Т.е. немалая часть веса птицы передавалось бы именно к стенкам...
и весы снизу это дело не измерили бы...
|
|
|
|
|
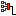 Записан
Записан
|
|
|
|
KM
Профи
Старожил
    
Карма: +604/-10
 Offline Offline
Сообщений: 2654
|
Почему же "несжимаемое тело". Это может быть и воздух. Вот возьмите мою картинку (3-ю, где цилиндр). Поршень не падает на дно (т.е. неподвижен) за счет того, что опирается на сжатый воздух. Если сверху на поршень положить гирю, то поршень снова не упадет на дно, т.к. будет опираться на воздух, который сожмется еще сильнее. И если цилиндр стоит на весах, они зафиксируют изменение веса на +гирю, т.к. гиря опирается на поршень, поршень - на воздух, воздух - на дно, дно - на весы. Если бы вместо воздуха был вакуум, то опоры поршня бы не было и он бы тотчас упал на дно.
По поводу ускорения верно. Однако двигаться с ускорением можно только отталкиваясь от чего-либо, движущегося в противоположную сторону, согласны? (Я не беру в расчет случай изменения гравитации, например, если сверху поднести магнит). Отталикиваясь - т.е. создавая противоположно направленную силу той же величины.
Насчет размеров птицы и контейнера вопрос не понял. Но ответ - размеры значения не имеют, разумеется.
|
|
|
|
|
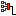 Записан
Записан
|
|
|
|
kondr
Активный участник
 
Карма: +0/-0
 Offline Offline
Сообщений: 199
|
Воздух циркулирует постоянно, птица представляет собой постоянный компрессор, она нагнетает воздух из верхней части в нижнюю по кругу. Разница в давлении у пола и потолка выше, чем была бы без птицы - у пола давление выше, на величину разряженности над птицей. Весь воздух давит вниз - на него действует сила притяжения земли.
Это же подтверждается из ссылки Алека:"Показания весов не изменятся, т.к. во время парения птичка все время должна отбрасывать воздух вниз, чтобы создавать подъемную силу, равную средней величине своего веса"
|
|
|
|
|
 Записан
Записан
|
|
|
|
KM
Профи
Старожил
    
Карма: +604/-10
 Offline Offline
Сообщений: 2654
|
Если прав КМ, это значит, что птица полностью опирается на дно вагона. А я вот думаю, что даже если давление внизу вагона и выше, чем наверху (хоть на чуточку), то это не значит что воздух давит только на пол вагона. Он по идее должен также давить сильнее и на стенки вагона, в участках ниже от птицы. Т.е. опорой птицы может являться упругое сопротивление стенок вагона, которое никак не отражается на показаниях весов... Почти так. Птица создает под собой давление воздуха, которое действует одинаково на дно и на стенки. Т.е. сила давления равномерно распределена по нижней части самой птицы, стенкам ниже птицы и дну. Но для того, чтобы не падать, птице нужны только вертикально направленные силы, которые давят снизу на птицу. Ровно такие же силы по величине, но направленные противоположно, давят на дно. И так как птица не ускоряется, они равны ее весу. Поэтому по сути птица совершает "избыточную" с ее точки зрения работу, гоняя воздух, который давит на стенки. Если бы воздух давил только на дно и саму птицу, ей было бы легче махать 
|
|
|
|
|
 Записан
Записан
|
|
|
|
Гoсть
Гость

|
Почему же "несжимаемое тело". Это может быть и воздух. Вот возьмите мою картинку (3-ю, где цилиндр). Поршень не падает на дно (т.е. неподвижен) за счет того, что опирается на сжатый воздух. Если сверху на поршень положить гирю, то поршень снова не упадет на дно, т.к. будет опираться на воздух, который сожмется еще сильнее. И если цилиндр стоит на весах, они зафиксируют изменение веса на +гирю, т.к. гиря опирается на поршень, поршень - на воздух, воздух - на дно, дно - на весы. Если бы вместо воздуха был вакуум, то опоры поршня бы не было и он бы тотчас упал на дно.
Верно. Но только поршень не тратит энергию для противодействия g, а газ (рабочее тело) не имеет возможности перетекать из зоны под поршнем, в зону над поршнем. Под действием массы поршня и гири, за счет тяготения, воздух сожмется до состояния равновесия. До состояния несжимаемости достаточной в данных условиях. Сжатый воздух (при условии герметичности) станет опорой. Просто воздух под поршнем, это отдельная изолированная система. По поводу ускорения верно. Однако двигаться с ускорением можно только отталкиваясь от чего-либо, движущегося в противоположную сторону, согласны? (Я не беру в расчет случай изменения гравитации, например, если сверху поднести магнит). Отталикиваясь - т.е. создавая противоположно направленную силу той же величины.
Согласен. Согласен. Согласен. Птица отталкивается от молекул воздуха, которые возвращаются снова в зону "захвата". Потому что птица не поршень, а вагон не цилиндр. Насчет размеров птицы и контейнера вопрос не понял. Но ответ - размеры значения не имеют, разумеется.
В вашей модели - птица является поршнем. Зазор крыло-стена минимальный. В моем понимании, зазор на порядки больше размеров птицы.
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
|
Светлана
Старожил
  
Карма: +11/-2
 Offline Offline
Сообщений: 12941
|
Можно, добавлю?
Давайте представим, что птиц парализовало в полёте. Они перестали работать крыльями, но система ещё не в равновесии. Весы ещё показывают меньшее значение, чем до взлёта. Что дальше? Птицы падают вниз с силой, равной mg (за вычетом сопротивления воздуха), и, только когда они упадут, система станет равновесной. Весы покажут первоначальное значение: mвагона + mвоздуха + mптиц.
И, если можно, попробуем наоборот. Пусть вместо птиц в воздухе висели бы модели, не производящие работы крыльями. Их пришлось бы наполнить газом с меньшей, чем воздух плотностью, чтобы их вес был бы уравновешен силами выталкивания (пример Сергея Кейза). Но система считалась бы равновесной, как только сила выталкивания уравновесила бы вес модели с лёгким газом. То есть, в начале эксперимента нужно было бы наоборот приложить силу, прижимающую модель ко дну. Снова система не в равновесии. Убрали силу - модель взмыла на определённую высоту (довольно значительную по сравнению с её размерами). Система приобрела равновесное состояние, а показания весов по сравнению с показаниями в начале эксперимента уменьшились.
С уважением, Светлана.
|
|
|
|
|
 Записан
Записан
|
|
|
|
KM
Профи
Старожил
    
Карма: +604/-10
 Offline Offline
Сообщений: 2654
|
Верно. Но только поршень не тратит энергию для противодействия g, а газ (рабочее тело) не имеет возможности перетекать из зоны под поршнем, в зону над поршнем. Неправильно  Энергию трятят (все, кто не поршень  ) не для противодействия g, а для перекачки воздуха с целью создания повышенного давления под собой. А поршень не тратит, т.к отверстий нет и уплотненный воздух и так не перекачивается вверх.
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
|
KM
Профи
Старожил
    
Карма: +604/-10
 Offline Offline
Сообщений: 2654
|
избыточную работу... хм.. тяжелый труд у птиц...
птице совсем не важно какая форма у дна и стен вагона. И как они далеко. Ей надо оттолкнуться от воздуха под ней. Для этого ей надо создать силу под крылом равную силе тяготения.
Получив импульс, молекула воздуха начнет бить соседние, а те в свою очередь уже с меньшей скоростью своих соседей, и импульс начнёт гаситься на трение самого воздуха, на увеличение средней кинетической скорости молекул (воздух нагреется) и в итоге весь остаточный импульс ударится, если дотянет, об стенки и дно вагона. Весы могут чувствовать только импульс исходящий от тех молекул которые дотянули до дна. Если верить Вам, то птице на высоте 300 метров нужно создать такой ветер, который дотянет до земли. Нелогично это как-то.
Все логично, просто масштабы разные. Птица очень маленькая, а высота большая, поэтому птице понадобится ооочень много времени, чтобы поток воздуха долетел до земли, но в физической модели так оно и будет. А вот если заменить птицу на вертолет, а 300 метров - на 3, тогда ведь у вас не будет совмнений в огромной силе давления воздушного потока на поверхность земли? А ведь физические модели в обоих случаях абсолютно одинаковые.
|
|
|
|
|
 Записан
Записан
|
|
|
|
|
|
|
| Интересное |
|
Ссылки |
Автор |
Ответов |
Просмотров |
Последнее сообщение |

|

|
→ Выбор, покупка стальной двери или замка
|
skyhome
|
65
|
35135
|
 24 ноя, 2011, 22:22
24 ноя, 2011, 22:22
от Oleg1601
|

|

|
→ Главный форум
|
Oleg2012
|
14
|
5663
|
 07 июн, 2012, 18:21
07 июн, 2012, 18:21
от jasv
|

|

|
→ Главный форум
|
KonstantinK
|
7
|
5043
|
 24 сен, 2012, 19:34
24 сен, 2012, 19:34
от KonstantinK
|

|

|
→ Выбор, покупка стальной двери или замка
|
s.aleks
|
1
|
2283
|
 22 окт, 2012, 10:05
22 окт, 2012, 10:05
от Сергей Мещеряков
|

|

|
→ Изготовление и дублирование ключей
|
Alexdy
|
5
|
1280
|
 04 дек, 2018, 18:34
04 дек, 2018, 18:34
от Alexdy
|
|








 Цитировать
Цитировать Добавить к цитированию
Добавить к цитированию Удалить из цитирования
Удалить из цитирования Записан
Записан


 ). "Локальных зон" в нашей системе не существует, т.к. мы договорились не рассматривать неуравновешенную систему. Теперь смотрите на картинку. Вы пытаетесь применить закон Паскаля ко всему цилиндру, но это неверно! Цилиндр разделен птицей на две части.
). "Локальных зон" в нашей системе не существует, т.к. мы договорились не рассматривать неуравновешенную систему. Теперь смотрите на картинку. Вы пытаетесь применить закон Паскаля ко всему цилиндру, но это неверно! Цилиндр разделен птицей на две части. 